Domena funkcije arcsin
\(f(x,y)=arcsin5\Big(1-2\Big(\frac{x-y}{x+y}\Big)^2\Big)\), \(D_f=?\)
\[-1\leq1-2\Big(\frac{x-y}{x+y}\Big)^2\leq1\]
\[-2\leq-2\Big(\frac{x-y}{x+y}\Big)^2\leq0 \quad \bigg/:(-2)\]
\[1\geq\Big(\frac{x-y}{x+y}\Big)^2\geq0\]
\[\Big(\frac{x-y}{x+y}\Big)^2\leq1 \quad \bigg/^\sqrt{}\]
\[\Bigg|\frac{x-y}{x+y}\Bigg|\leq1\]
\[\text{1. slučaj}\]
\[\frac{x-y}{x+y}\geq-1 \quad \text{…}\]
\[\frac{x}{x+y}\geq0\]
\[\text{1.1. slučaj }\]
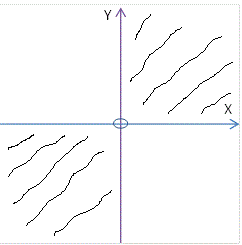
\[\text{$x\geq0$ $\quad$ i $\quad$ $y>-x$}\]
\[\text{Slika 1.1}\]
 \[\text{1.2. slučaj}\]
\[\text{$x\leq0$ $\quad$ i $\quad$ $y \lt -x$}\]
\[\text{Slika 1.2}\]
\[\text{1.2. slučaj}\]
\[\text{$x\leq0$ $\quad$ i $\quad$ $y \lt -x$}\]
\[\text{Slika 1.2}\]
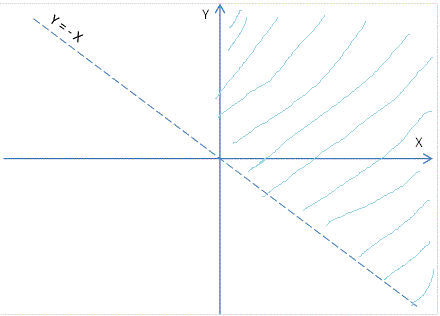
 \[\text{ Riješenje slučaja 1. je unija slike 1.1 i slike 1.2, a to se vidi na sljedećoj slici.}\]
\[\text{Slika 1}\]
\[\text{ Riješenje slučaja 1. je unija slike 1.1 i slike 1.2, a to se vidi na sljedećoj slici.}\]
\[\text{Slika 1}\]
 \[\text{2. slučaj}\]
\[\frac{x-y}{x+y}\leq1 \quad \text{…}\]
\[\frac{y}{x+y}\geq0\]
\[\text{2.1. slučaj}\]
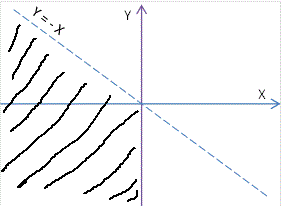
\[\text{$y\geq0$ $\quad$ i $\quad$ $y \gt -x$}\]
\[\text{Slika 2.1}\]
\[\text{2. slučaj}\]
\[\frac{x-y}{x+y}\leq1 \quad \text{…}\]
\[\frac{y}{x+y}\geq0\]
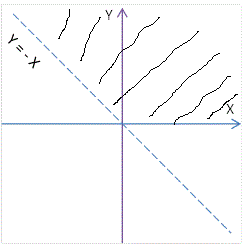
\[\text{2.1. slučaj}\]
\[\text{$y\geq0$ $\quad$ i $\quad$ $y \gt -x$}\]
\[\text{Slika 2.1}\]
 \[\text{2.2. slučaj}\]
\[\text{$y\leq0$ $\quad$ i $\quad$ $y \lt -x$}\]
\[\text{Slika 2.2}\]
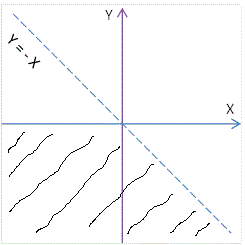
\[\text{2.2. slučaj}\]
\[\text{$y\leq0$ $\quad$ i $\quad$ $y \lt -x$}\]
\[\text{Slika 2.2}\]
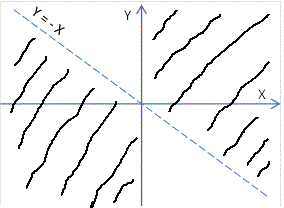
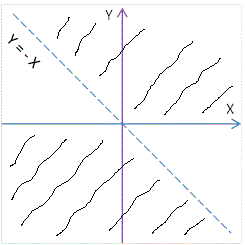
 \[\text{Riješenje slučaja 2. je unija slike 2.1 i slike 2.2, a to se vidi na sljedećoj slici.}\]
\[\text{Slika 2}\]
\[\text{Riješenje slučaja 2. je unija slike 2.1 i slike 2.2, a to se vidi na sljedećoj slici.}\]
\[\text{Slika 2}\]
 \[\text{Konačno riješenje je presjek 1. slučaja i 2. slučaja}\]
\[\text{Slika}\]
\[\text{Konačno riješenje je presjek 1. slučaja i 2. slučaja}\]
\[\text{Slika}\]