Normalna distribucija
Pretpostavimo da prinos stabla prati normalnu distribuciju sa srednjom vrijednosti 30 kg i srandardnom devijacijom 3 kg. Kolika je vjerojatnost da nasumično odabrano stablo smokve ima prinos veći od 26.4 kg?
Koristeći R jezik to se izračuna brzo sa ovom naredbom. \[1-pnorm(26.4, 30, 3) = 0.8849\]
A bez pomoći računala to bi išlo ovako. Traži se \(P(X>26.4)\) gdje X znači prinos stabla. Zbog toga što X prati normalnu distribuciju možemo je svesti na standardu (jediničnu) normalnu distribuciju supstitucijom \(\Phi = \frac{x-\overline{x}}{\sigma} = \frac{26.4-30}{3} = -1.2\)
\[P(X>26.4) = 1-P(X<26.4) = 1-\Phi(-1.2)\]
Pogledajmo sliku standarde normalne distribucije.
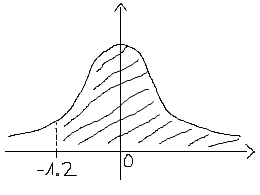Naše rješenje je iscrtkana površina ispod krivulje. Da bi to izračunali koristimo se tablicom standarde normalne distribucije koju možete
nači na internetu. Ali u njoj nema negativni 1.2, već samo pozitivni, pa iz te tablice vidimo \(\Phi(1.2) = 0.8849\).
Međutim na dnu te tablice vidimo kako treba raditi s negativnim argumentima. \[\Phi(-1.2) = 1-\Phi(-(-1.2)) = 1-\Phi(1.2)\] I sada uvrstimo ovo u početak i imamo rješenje: \[1-\Phi(-1.2) = 1-(1-\Phi(1.2)) = \Phi(1.2) = 0.8849\]