Dvostruki integral 1
Izračunajte dvostruki integral \(\iint_D \frac{1-x^2-y^2}{1+x^2+y^2} \,dx\,dy\) na području \(D=\{(x, y) \in \Bbb R^2 \mid x^2+y^2 \leq 1, \quad y \geq 0\}\)
Najprije lijepo nacrtamo sliku područja.
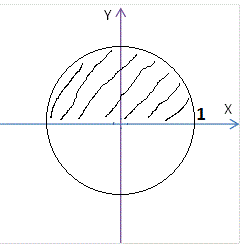Očito trebamo prijeći na eliptične koordinate.
\[
\begin{cases}
x = \rho cos \varphi\
y = \rho sin \varphi
\end{cases}
\quad
0 < \rho < 1,
\quad
0 < \varphi < \pi
\]
Sad kad imamo eliptične koordinate i znamo granice možemo rješavati.
\[\int_{0}^{1} \,d\rho \int_{0}^{\pi} \frac{1-\rho^2 cos^2 \varphi-\rho^2 sin^2 \varphi}{1+\rho^2 cos^2 \varphi+\rho^2 sin^2 \varphi} \cdot \rho \,d\varphi\] \[\int_{0}^{1} \rho \,d\rho \int_{0}^{\pi} \frac{1-\rho^2}{1+\rho^2} \,d\varphi\] \[\int_{0}^{1} \rho \cdot \frac{1-\rho^2}{1+\rho^2} \,d\rho \cdot \int_{0}^{\pi} \,d\varphi\] Uvodimo supstituciju \(\rho^2 = t\), pa to deriviramo i dobijemo \(2 \rho \,d\rho = \,dt\)
I granice se mijenjaju pa imamo \(0 < \rho < 1 \quad\) i \(\quad 0 < \varphi < 1\)
\[\frac{1}{2}\int_{0}^{1} \frac{1-t}{1+t} \,dt \cdot \Big(\varphi\Big\vert_{0}^{\pi}\] \[\frac{1}{2}\int_{0}^{1} \frac{1+t-2t}{1+t} \,dt \cdot \pi\] \[\frac{\pi}{2}\Big(\int_{0}^{1} \,dt - 2\int_{0}^{1}\frac{t}{1+t} \,dt \Big)\] \[\frac{\pi}{2}\Big(1 - 2\int_{0}^{1}\frac{1+t-1}{1+t} \,dt \Big)\] \[\frac{\pi}{2}\bigg(1 - 2\Big(\int_{0}^{1} \,dt - \int_{0}^{1}\frac{\,dt}{1+t} \Big)\bigg)\] \[\frac{\pi}{2}\bigg(1 - 2 + 2\Big(ln(1+t)\Big\vert_{0}^{1}\bigg)\] \[\frac{\pi}{2}\Big(-1 + 2ln2\Big)\] \[\frac{\pi}{2}\Big(ln4-1\Big)\]