Uvjetna vjerojatnost i venov diagram 1
U istraživanju genetike otpornosti na bolesti, proučavan je uzorak od više tisuća nasumično odabranih biljaka pšenice. Kod jednog dijela biljaka 0,22 zabilježen je gen za otpornost R1. Kod jednog dijela biljaka 0,28 zabilježeno je kako su otporne na napad gljivica tijekom ljeta. Kod jednog dijela biljaka 0,18 utvrđeno je da imaju gen R1 i da su otporne na gljivice. Pretpostavimo kao su gore navedeni postotci vjerojatnosti. Koja je vjerojatnost da ako je biljka otporna na napad gljivica ne nosi gen R1?
Znači treba izraćunati \(P(O/\overline{R1})\).
\(O\) znači otpornost, \(R1\) znači da ima gen, a \(\overline{R1}\) da nema gen R1.
\[ P(O/\overline{R1}) = \frac{P(O\cap\overline{R1})}{P(\overline{R1})} = \frac{P(O\cap\overline{R1})}{1-P(R1)} = \frac{P(O\cap\overline{R1})}{1-0.22} = \frac{P(O\cap\overline{R1})}{0.78} \]
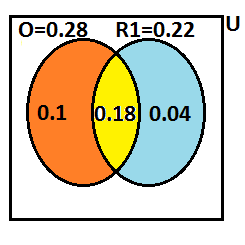
Sada moramo izračunati brojnik. Mi imamo \(P(O\cap R1) = 0.18\) i \(P(O)=0.28\). Poslužiti ćemo se venovim dijagramom.
Ima jedna formula \(P(A \cup B)=P(A)+P(B)-P(A \cap B)\). Pa onda vrijedi:
\[P(O\cap\overline{R1}) = P(O)+P(\overline{R1})-P(O \cup\overline{R1})\] \[ = 0.28+0.78-P(O \cup\overline{R1})\] Da bi izačunali \(P(O \cup\overline{R1})\) pogledajmo sliku. Zaključujemo da je to cijela ona slika bez plavog dijela, a to je \(1-0.04\). Idemo dalje. \[ = 0.28+0.78-(1-0.04) = 0.28+0.78-0.96 = 0.1\] I sada se vratimo na početak i dovršimo. \[P(O/\overline{R1}) = \frac{0.1}{0.78} = 0.1282051\]