FPR, FNR i prevalencija statističkog testa u medicini
U određenom testu za korištenje marihuane, lažno pozitivna stopa (false positive rate FPR) je 0.01, a lažno negativna stopa (false negative rate FNR) je 0.06. Prevalencija (učestalost) korištenja marihuane u nekoj populaciji je 0.12.
Osoba je imala pozitivan test na korištenje marihuane. Kolika je vjerojatnost da je doista i koristila marihuanu?
Znači treba izračunati PPV testa. Za ovaj zadatak bi bilo dobro pogledati zadatak od 17 Nov 2018. I za ovaj zadatak nam
treba tablica. Neka je T pozitivan test, T’ negativan test, C (eng. condition tj. stanje) da je uzimao marihuanu, a C’ da
nije uzimao marihuanu. Iz prošlog zadatka znamo da je \(\alpha = FPR = 0.01\) i da je \(\beta = FNR = 0.06\). Novost je da prevalenciju
označavamo sa \(\gamma = 0.12\). Pa napravimo tablicu i rješimo PPV.
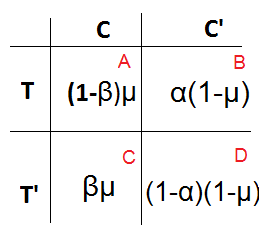\[PPV = \frac{A}{A+B} = \frac{(1-\beta)\gamma}{(1-\beta)\gamma+\alpha(1-\gamma)}\]
\[= \frac{(1-0.06)0.12}{(1-0.06)0.12+0.01(1-0.12)}\]
\[= 0.9276316\]